座標変換行列の導出
※これは過去のブログ記事を再掲したものです。
地心直交座標系から局所座標系への変換に使用する座標変換行列を導出してみたのでメモしておきます。
まずは簡単な説明から。
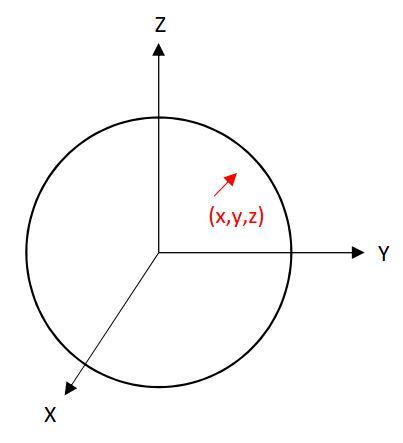
「地心直交座標系」は地球の重心を原点として、赤道上の経度0°方向をX軸、東経90°方向をY軸、原点から地心軸方向をZ軸とする座標系です。
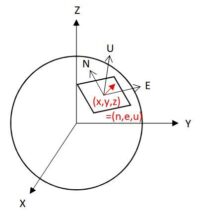
これに対して「局所座標系」は地球上の任意の点を基準に北方向をN軸、東方向をE軸、高さ方向をU軸とする座標系です。
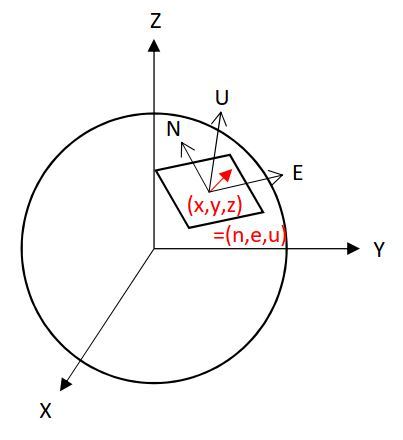
地心直交座標系におけるベクトル(x,y,z)を局所座標系におけるベクトル(n,e,u)として表現することで、任意地点での平面的な方向(n,e)や高さ(u)を知ることができます。
※質問頂きましたので、以下、補足します。
GNSS測量では地球の重心を原点にした地心直交座標が計算に使用されるため、誤差の表現には向いていません。(地心軸や経度0度、経度90度の方向にそれぞれ誤差がいくらありますと言われても、わかりにくいですよね。)
そのため観測位置付近での平面及び高さの誤差が表現できる局所座標系に変換して、精度を確認しています。(北に5mm、東に10mm、高さ方向に20mmなど)
1.二次元の回転
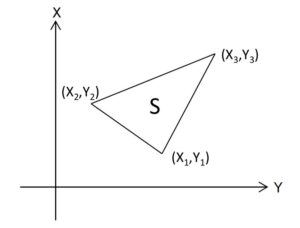
まずは二次元での座標系の回転について。
XY座標系で(x,y)の大きさをもつベクトルについて座標系の回転を考えてみます。
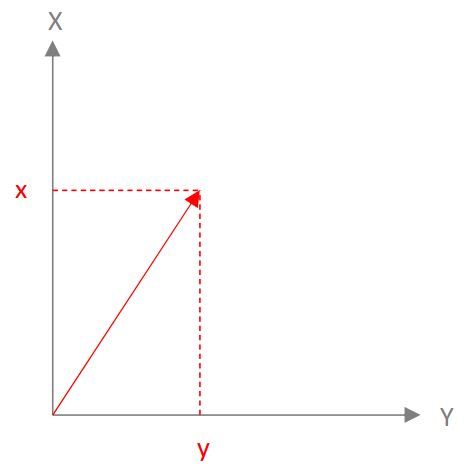
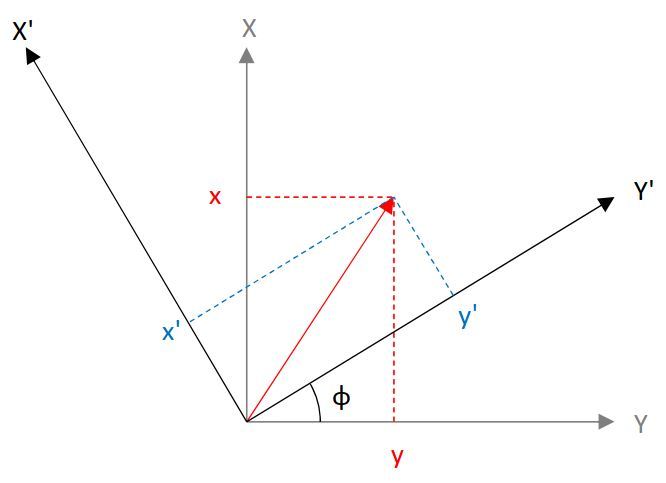
XY座標系をΦだけ回転させたX’Y’座標系でのベクトルの大きさ(x’,y’)は…
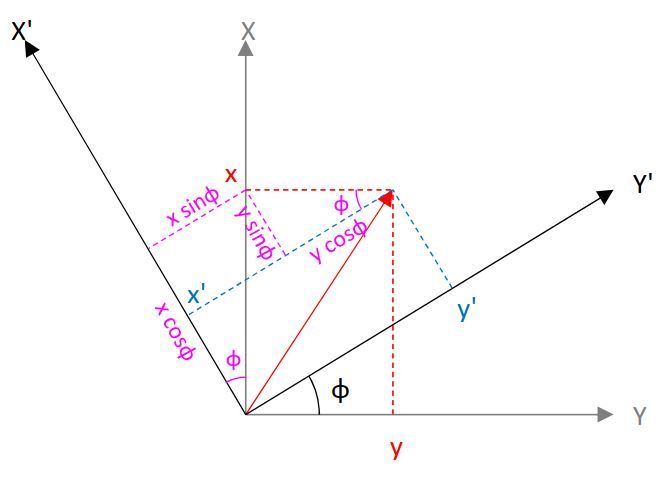
次のように計算できます。
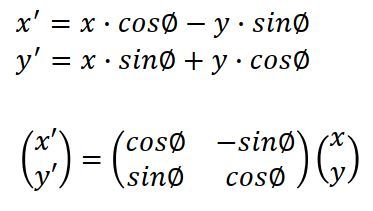
2.三次元の回転
以上をベースに次のような三次元直交座標系の回転について考えてみます。
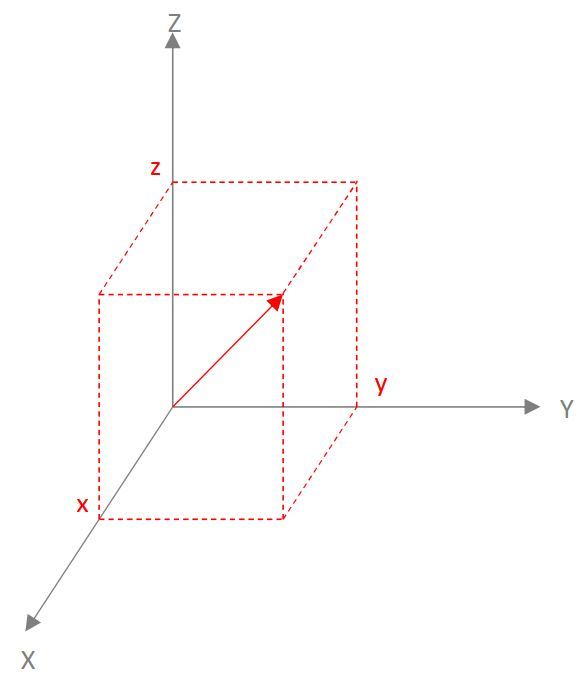
2-1.Z軸の回転
Z軸を固定して経度λだけ回転します。
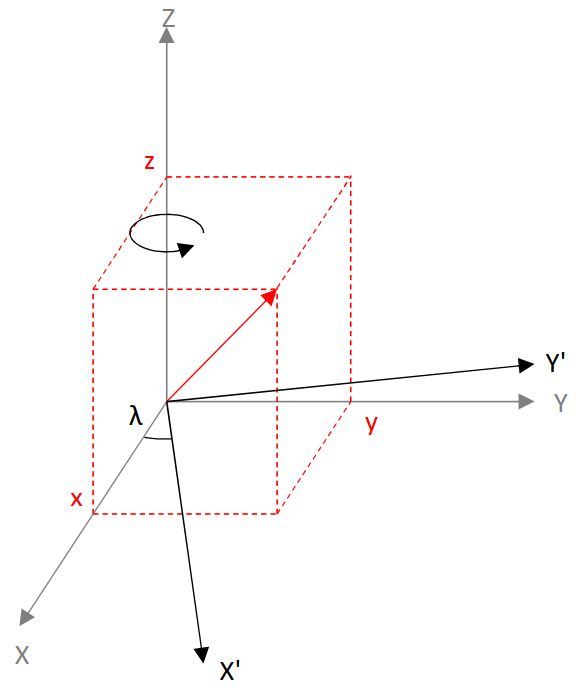
視点をZ軸方向に移動すると、こんな感じ。
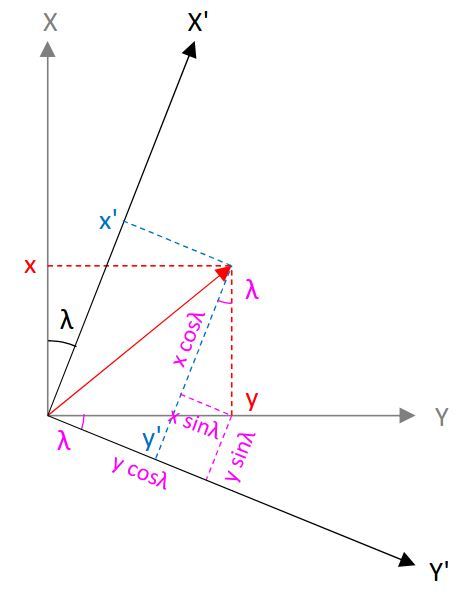
計算式は以下の通り。
XYの回転は二次元の時と同じ、Z軸は回転しないのでそのままです。
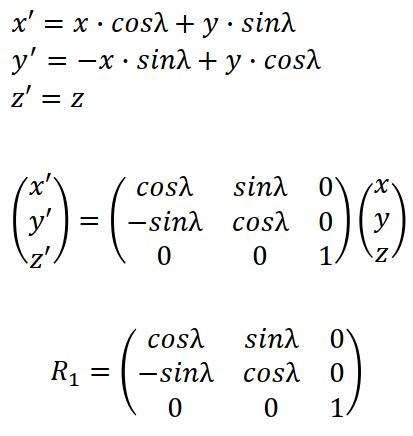
2-2.Y軸の回転
次にY’軸を固定して、Z’軸の傾きが緯度Φとなるように回転させます。
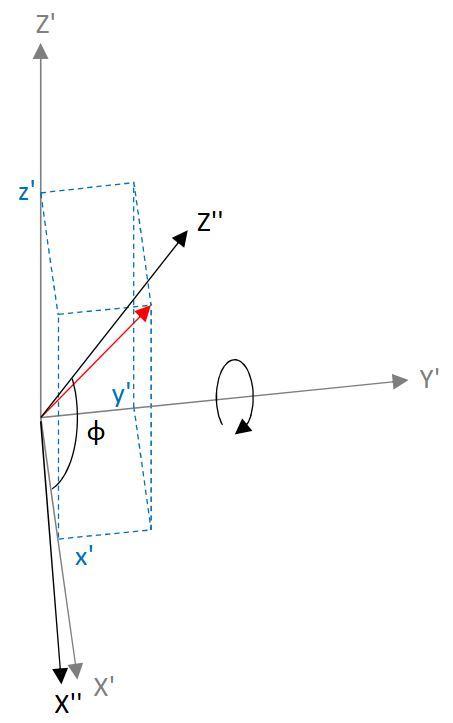
先ほどと同様に視点をY’軸方向に移動します。
回転量はπ/2-Φであることに注意して下さい。下図のように考えます。

計算式は以下の通り。
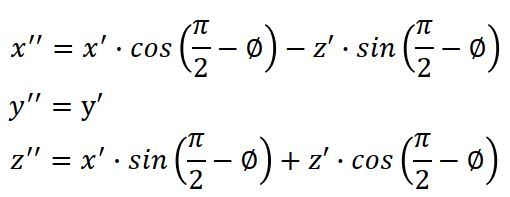
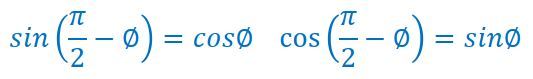
を用いると、以下のようになります。
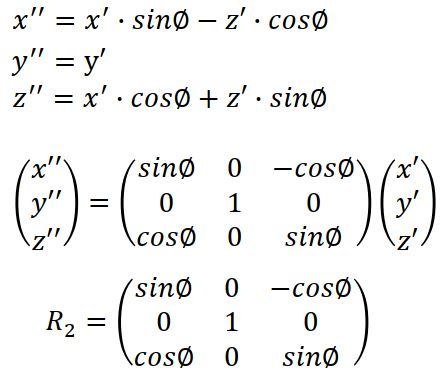
2-3.X軸の変換
2-1、2-2の変換により、X”軸は南方向が正になっています。
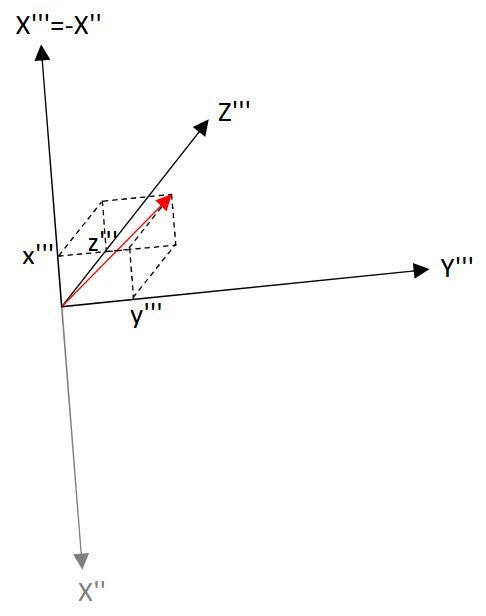
次の変換で、X”軸を北向きに補正します。
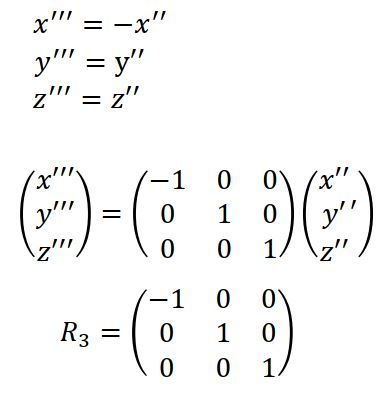
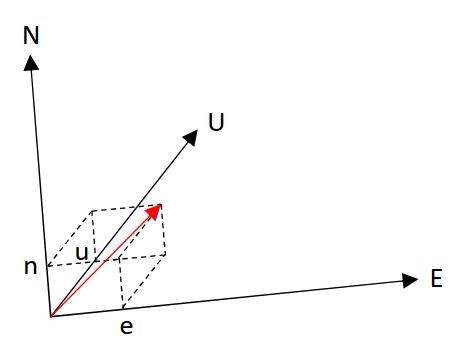
変換後の座標軸X”’、Y”’、Z”’をそれぞれN、E、Uに置き換えます。
3.座標変換行列
2-1から2-3で求めた変換行列R1、R2、R3をまとめて、座標変換行列を導きます。
計算式は以下の通りです。
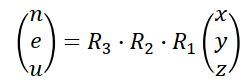
前から順番に計算していきます。
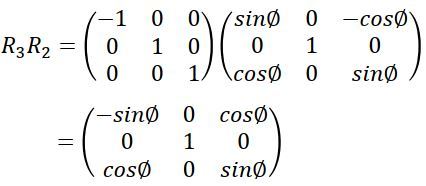
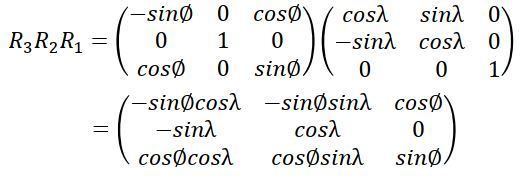
座標変換行列
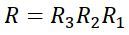
とおくと、
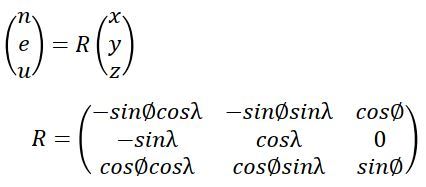
以下のページで実際に計算できるので、基準点成果作成の際にご利用ください。
地心直交座標系→局所座標系