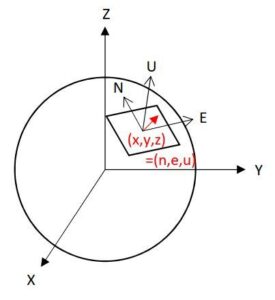
座標求積
※これは過去のブログ記事を再掲したものです。
時々お問い合わせ頂くので、今回は座標求積について記事を書くことにしました。
近年の測量による土地の区画は、一般的に測点と測点を順次結んで表現します。
座標求積とは、測点の位置を表す座標値から面積を求める方法です。
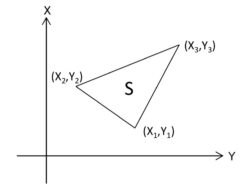
まずは下図のような三角形の面積Sについて考えてみます。
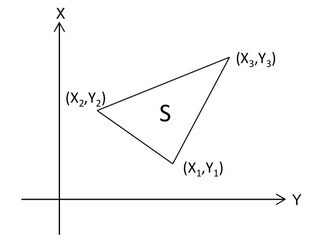
座標求積ではいくつかに分けた台形の面積を計算します。
計算する台形の数は求積する図形の辺の数と同じです。この例では三角形を求積するので、台形の数は3個です。
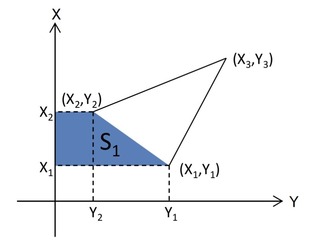
台形の面積は、以下の公式により計算できます。
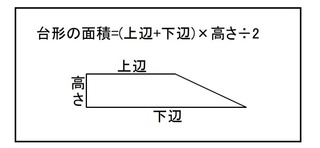
この公式を使って、各台形の面積を計算していきます。
①S1の面積
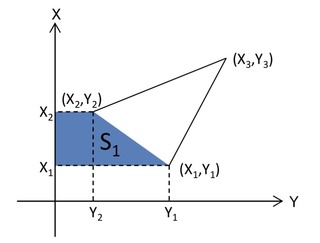
台形の面積に使用する上辺はY2、下辺はY1、高さはX1-X2です。
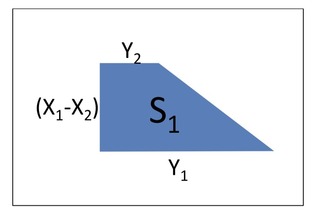
台形S1の面積は公式より、
S1=(Y2+Y1)×(X1-X2)÷2
※(X1-X2)は負(-)なので、S1は負(-)となります。
この時、高さ(X1-X2) は X1>X2 と X1<X2 とで正負(+-)が異なります。
必ず、Xn – Xn+1や、Xn+1-Xnなど、計算する順番を決めておきます。
この正負によって、各台形の面積の正負が決まります。この例では、Xn-Xn+1で計算をすすめます。
以下、同様に各台形の面積を求めます。
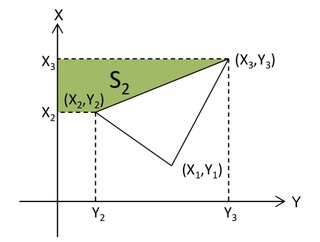
②S2の面積
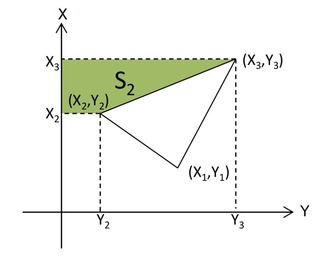
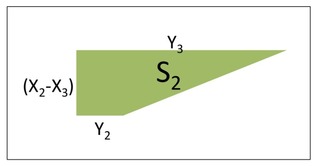
S2=(Y3+Y2)×(X2-X3)÷2
※(X2-X3)は負(-)なので、S2は負(-)となります。
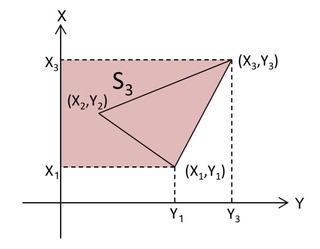
③S3の面積
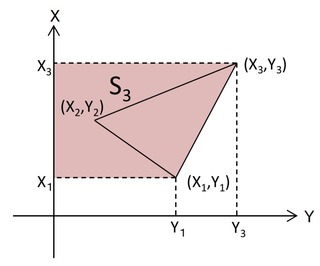
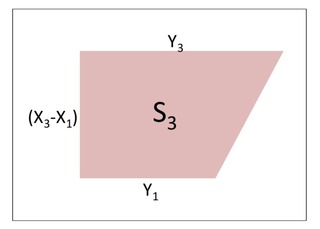
S3=(Y3+Y1)×(X3-X1)÷2
※(X3-X1)は正(+)なので、S3は正(+)となります。
①~③で計算した台形の面積を合計することで、Sの面積が求められます。
S =(-)S1+(-)S2+S3 =S3-S1-S2
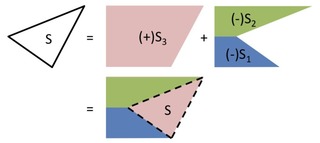
以上のように、台形の面積の合計から任意の図形の面積が計算できます。
①~③の式を整理し一般化します。
①’
S1=(Y2+Y1)×(X1-X2)÷2
=(Y2X1-Y2X2+Y1X1-Y1X2)÷2
②’
S2=(Y3+Y2)×(X2-X3)÷2
=(Y3X2-Y3X3+Y2X2-Y2X3)÷2
③’
S3=(Y3+Y1)×(X3-X1)÷2
=(Y3X3-Y3X1+Y1X3-Y1X1)÷2
S=S1+S2+S3なので、
S =(Y2X1-Y2X2+Y1X1-Y1X2 +Y3X2-Y3X3+Y2X2-Y2X3 +Y3X3-Y3X1+Y1X3-Y1X1)÷2
=(Y2X1-Y1X2+Y3X2-Y2X3-Y3X1+Y1X3)÷2
={(Y2-Y3)X1+(Y3-Y1)X2+(Y1-Y2)X3}÷2
この例は三角形についての式なので、n角形の式として整理すると、
S=Σ(Yn+1-Yn-1)Xn÷2
となります。
下の例で実際に計算してみます。
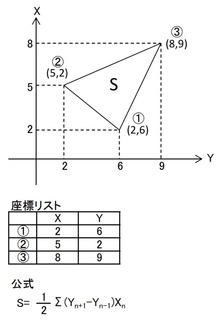
An=(Yn+1-Yn-1)Xnとおくと、
A1=(Y②-Y③)・X①=(2-9)×2=-14
A2=(Y③-Y①)・X②=(9-6)×5=15
A3=(Y①-Y②)・X③=(6-2)×8=32
S=(A1+A2+A3)÷2
=(-14+15+32)÷2
=33÷2
=16.5